Rodrigues' Rotation Formula

Sources: 1 2 3

I stumbled upon this when checking my camera calibration. I could see that depending on the angle of the camera upon the X axis, a stationary ArUco mark would fluctuate a lot on it’s Z-axis position. This is related to camera backward projection, SeaClear.

The issue was fixed through Rodrigues’ Rotation Formula in opencv:

rmat, _ = cv2.Rodrigues(rvec)  
rmat_inv = rmat.T  
tvec_inv = -np.dot(rmat_inv, tvec.T)  
rvec_inv, _ = cv2.Rodrigues(rmat_inv)  
return rvec_inv, tvec_inv.T

So, I want to document this algorithm and see what exactly it does and why it fixed the issue. From what I understood, it succeeds in computing the camera pose camera backward projection and not the ArUco marker’s pose. (I could definitely phrase that better)

Related To: Axis-Angle Representation (Rotation Vector), Mechanization, Lie Algebra

Rotation Vector to Rotation Matrix

Rodrigues' Formula

The conversion from rotation vector to rotation matrix is shown by Rodrigues’ formula. The result of the conversion is the follo

$$R=\cos \theta I+(1-\cos \theta )n{n}^T+\sin \theta [n{]}_{\mathbf{x}}$$

where

• R is the rotation matrix
• the rotation axis has unit length vector n and angle $\theta$
• ^ or $[{]}_{\mathbf{x}}$ is the skew-symmetric operator

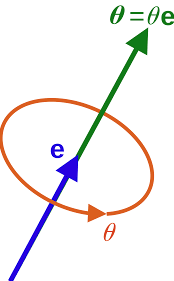
Since the rotation axis does not change after the rotation, we have Rn $=$ n. Therefore, the axis n is the eigenvector corresponding to the matrix R’s eigenvalue 1.

Python Implementation: Extracting 3D position from accelerometer dataset, with Rodrigues’ Rotation Formula implemented in lie algebra. Available here.

def integrate_3d_trajectory(accel, gyro, timestamps, calibrate = False, constant_velocity = False):
 
	if calibrate: # Calibrated values
		accel = (accel - b_a) * (1 + s_a)
		gyro = (gyro - b_g) * (1 + s_g)
 
	dt = np.diff(timestamps)
	n = len(timestamps)
	pos_nav_frame = np.zeros((n, 3))
	vel_nav_frame = np.zeros((n, 3))
	R_nb = np.eye(3) # This is the Rotation Matrix every dt. Going from body to nav.
	g = np.array([0, 0, 9.81]) # To compensate for gravity vector.
 
  
 
	for i in range(1, n):
		roll_rate = gyro[i-1, 0] # X-Axis
		pitch_rate = gyro[i-1, 1] # Y-Axis
		yaw_rate = gyro[i-1, 2] # Z-Axis
		current_dt = dt[i-1]
 
		theta_vector = np.array([roll_rate, pitch_rate, yaw_rate]) * current_dt
		phi = np.linalg.norm(theta_vector)
		theta_skew = np.array([[0, -theta_vector[2], theta_vector[1]],
		[theta_vector[2], 0, -theta_vector[0]],
		[-theta_vector[1], theta_vector[0], 0]])
 
		if phi < 1e-9:
			R_exp = np.eye(3) # Avoid division by zero in case of no rotation.
		else:
			R_exp = (np.eye(3) + (np.sin(phi) / phi) * theta_skew + ((1 - np.cos(phi)) / phi**2) * np.dot(theta_skew, theta_skew))
 
		R_nb = R_nb @ R_exp
		specific_force_body = accel[i-1] # f = a - g
		specific_force_nav = R_nb @ specific_force_body # f
		accel_nav_linear = specific_force_nav - g # a
		prev_vel = vel_nav_frame[i-1]
		current_vel = prev_vel + accel_nav_linear * current_dt
 
		if constant_velocity:
			vel_nav_frame[i] = R_nb @ np.array([1.0, 0.0, 0.0])
		else:
			vel_nav_frame[i] = current_vel
			pos_nav_frame[i] = pos_nav_frame[i-1] + prev_vel * current_dt
 
	return pos_nav_frame