Iterative Closest Point (ICP)

From Indoor 3D: Overview on Scanning and Reconstruction Methods, chapter 3.5.2.

Process

1. Take two scans of 2D/3D point cloud
2. Compute the center of mass and shift the point clouds on top of each other

We want to find the transformation (R,t) between model set $\hat{M}$ and data set $\hat{D}$. The problem is cast as a least squares minimization problem, so that we want to minimize the cost function

$$\min E(R,t)=\frac{1}{N}\sum _{i=1}^N\mid m_i-(R{d}_i+t){\mid }^2$$

where for each point $m_i\in M\subset \hat{M}$ there is a closest point $d_i\in D\subset \hat{D}$.

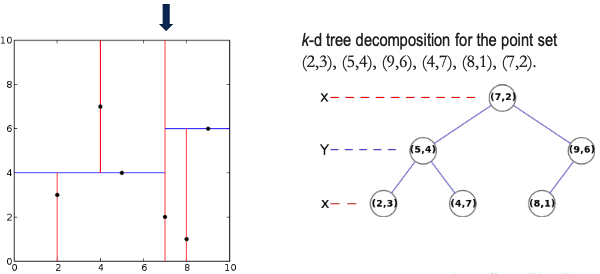
Computation of the closest point is the most computationally expensive step in ICP. Therefore, we don’t loop over all points in d to find a closest point for $m_{i}O(n^2)$, but we search with optimized k-trees, $O(N\log (N))$.

• k-dimensional tree is a space-partitioning data structure for organizing points in a k-dimensional space
• each point of the kd tree is k-dimensional and divides the space in two for the chosen direction.

Normalize w.r.t. the center of mass of each point cloud:

$$c_m=\frac{1}{N}\sum _{i=1}^N{m}_i$$ $$c_d=\frac{1}{N}\sum _{i=1}^N{d}_i$$

Then we can rewrite the cost function as:

$$\min E(R,t)=\frac{1}{N}\sum _{i=1}^N\mid m_i^{\prime }-R{d}_i^{\prime }-(t-c_m+R{c}_d){\mid }^2$$

where

• $m_i=m_i^{\prime }-c_m$
• $d_i=d_i^{\prime }-c_d$
• we denote $\tilde{t}=t-c_m+R{c}_d$

After we rearrange the terms, we get

$$\min E(R,t)=\frac{1}{N}\sum _{i=1}^N|m_i^{\prime }-R{d}_i^{\prime }{|}^2-2\frac{1}{N}\tilde{t}\cdot \sum _{i=1}^N(m_i^{\prime }-R{d}_i^{\prime })+\frac{1}{N}\sum _{i=1}^N{\tilde{t}}^2$$

where we divided the rotation and translation!

• We want to minimize this: $\frac{1}{N}{\sum }_{i=1}^N|m_i^{\prime }-R{d}_i^{\prime }{|}^2$
• The second term $2\frac{1}{N}\tilde{t}\cdot {\sum }_{i=1}^N(m_i^{\prime }-R{d}_i^{\prime })=0$ since all values refer to centroid.
• The third term $\frac{1}{N}{\sum }_{i=1}^N{\tilde{t}}^2$ has its minimum when $\tilde{t}=0$ or $t=c_m-R{c}_d$

Therefore, the algorithm needs to only minimize the first term, i.e.

$$\min E(R,t)\sim \frac{1}{N}\sum _{i=1}^N|m_i^{\prime }-R{d}_i^{\prime }{|}^2$$

The optimal solution is calculated by matrix factorization, $R=V{U}^T$ using SVD (Singular Value Decomposition).

We consider the $3\times 3$ cross correlation matrix $\mathbf{H}=\mathbf{U\Lambda }{\mathbf{V}}^T$

$$\mathbf{H}=\sum _{i=1}^N{\mathbf{m}}_i^{\prime T}{\mathbf{d}}_i^{\prime }=\left(\begin{array}{ccc}{S}_{xx}& S_{xy}& S_{xz}\\ S_{yx}& S_{yy}& S_{yz}\\ S_{zx}& S_{zy}& S_{zz}\end{array}\right)$$

where

• $S_{xx}={\sum }_{i=1}^N{m}_{x,i}^{\prime }{d}_{x,i}^{\prime }$,
• $S_{xy}={\sum }_{i=1}^N{m}_{x,i}^{\prime }{d}_{y,i}^{\prime }$,
• $S_{xz}={\sum }_{i=1}^N{m}_{x,i}^{\prime }{d}_{z,i}^{\prime },$
• $\dots$

contain the information of the 3D points in a stacked form