Multiple View Geometry in Computer Vision

You can find the book authored by Richard Hartley and Andrew Zisserman in .pdf format here on GitHub

The main points of interest are Camera Pose Estimations(Chapters 6.1, 6.2) and Coordinate Frames and Homogeneous Transformations(Chapter 7.2)

A camera is a mapping between the 3D world (object space) and a 2D image

For study, it references the pinhole camera model.

Central projection using homogeneous coordinates.

If the world and image points are represented by homogeneous vectors, then central projection is very simply expressed as a linear mapping between their homogeneous coordinates.

So, the last equation from pinhole camera model becomes:

$$\left(\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right)\mapsto \left(\begin{array}{c}fX\\ fY\\ Z\end{array}\right)=\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left(\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right)$$

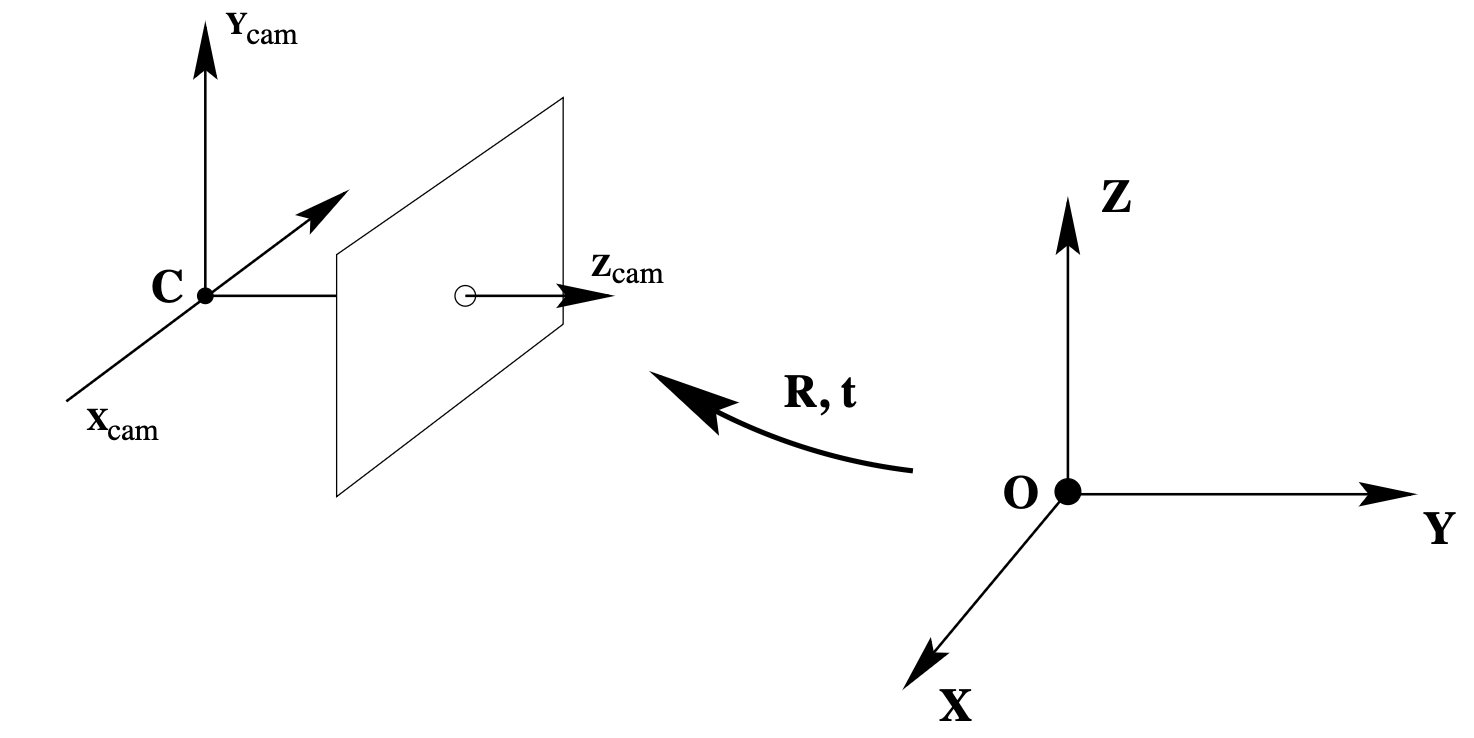
Camera Rotation and Translation

In general, points in space will be expressed in terms of a different Euclidean coordinate frame, known as the world coordinate frame. The two coordinate frames are related via a rotation and a translation.

Skipping some formulas, we define the camera matrix as:

$$\mathbf{P}=\mathbf{K}\cdot [\mathbf{R}\mid \mathbf{t}]$$

where

$$\mathbf{t}=-\mathbf{R}\tilde{\mathbf{C}}$$

$\tilde{\mathbf{C}}$ represents the coordinates of the camera centre in the world coordinate frame (see figure above). Thus, to map a world point $X$ to image points $x$, we use $x=PX$. $R$ and $T$ come from aruco.py in my case.

Let $M=KR$

Finding the camera center

The camera center $C$ is the point for which $PC=0$. Numerically this right null-vector may be obtained from the SVD(Singular Value Decomposition) of $P$.

The camera centre is the 1-dimensional right null-space C of P, i.e. $PC=0$.

• Finite camera (M is not singular):

  $$\mathbf{C}=\left(\begin{array}{c}-{\mathbf{M}}^{-1}{\mathbf{p}}_4\\ 1\end{array}\right)$$

• Camera at infinity (M is singular):

  $$\mathbf{C}=\left(\begin{array}{c}\mathbf{d}\\ 0\end{array}\right)$$

  where d is the null 3-vector of M, i.e. $\mathbf{Md}=0$.

---

Column points

For $i=1,\dots ,3$, the column vectors ${\mathbf{p}}_i$ are vanishing points in the image corresponding to the $X$, $Y$, and $Z$ axes respectively.
Column ${\mathbf{p}}_4$ is the image of the coordinate origin.

---

Principal plane

The principal plane of the camera is ${\mathbf{P}}^3$, the last row of P.

---

Axis planes

The planes ${\mathbf{P}}^1$ and ${\mathbf{P}}^2$ (the first and second rows of P) represent planes in space through the camera centre, corresponding to points that map to the image lines $x=0$ and $y=0$ respectively.

---

Principal point

The image point ${\mathbf{x}}_0=\mathbf{M}{\mathbf{m}}^3$ is the principal point of the camera,
where ${\mathbf{m}}^{3\top }$ is the third row of M.

---

Principal ray

The principal ray (axis) of the camera is the ray passing through the camera centre C
with direction vector ${\mathbf{m}}^{3\top }$.
The principal axis vector is:

$$\mathbf{v}=\det (\mathbf{M}){\mathbf{m}}^3$$

It is directed towards the front of the camera.

---

Depth of Points

Let $\mathbf{X}=(X,Y,Z,T{)}^{\top }$ be a 3D point and $\mathbf{P}=\left[\mathbf{M}\mid {\mathbf{p}}_4\right]$ be a camera matrix for a finite camera.
Suppose:

$$\mathbf{P}(X,Y,Z,T{)}^{\top }=w(x,y,1{)}^{\top }$$

Then:

$$\text{depth}(\mathbf{X};\mathbf{P})=\frac{\text{sign}(\det \mathbf{M})\cdot w}{T\Vert {\mathbf{m}}^3\Vert }$$

is the depth of the point $\mathbf{X}$ in front of the principal plane of the camera.