Understanding rotational frames in 3D

Related to Coordinate Frame.

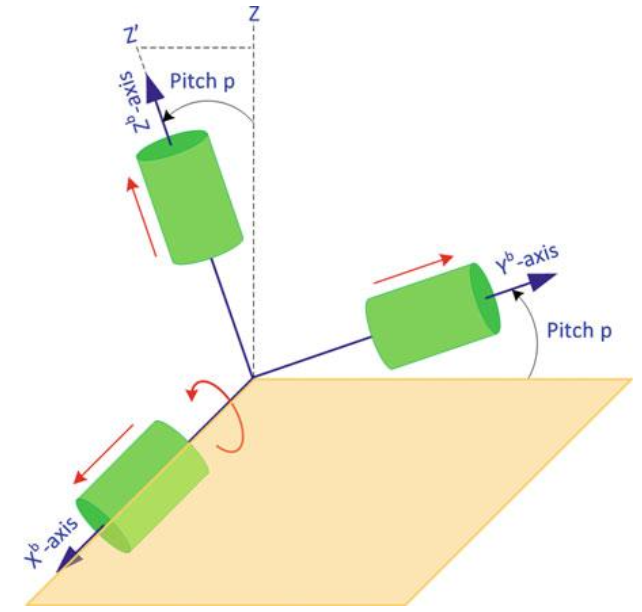
So I will explain on this example. We know the three rotational matrices.

R_x(p):

$$\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos p& -\sin p\\ 0& \sin p& \cos p\end{array}\right]$$

R_y(r):

$$\left[\begin{array}{ccc}\cos r& 0& \sin r\\ 0& 1& 0\\ -\sin r& 0& \cos r\end{array}\right]$$

R_z(ψ):

$$\left[\begin{array}{ccc}\cos \psi & -\sin \psi & 0\\ \sin \psi & \cos \psi & 0\\ 0& 0& 1\end{array}\right]$$

If I apply rotation on x axis (pitch), and then on y axis (roll) and at the end on z axis (yaw), the final rotational matrix will be

$$R=R_z(\psi )R_y(r)R_x(p)=\left[\begin{array}{ccc}\cos \psi \cos r& \cos \psi \sin r\sin p-\sin \psi \cos p& \cos \psi \sin r\cos p+\sin \psi \sin p\\ \sin \psi \cos r& \sin \psi \sin r\sin p+\cos \psi \cos p& \sin \psi \sin r\cos p-\cos \psi \sin p\\ -\sin r& \cos r\sin p& \cos r\cos p\end{array}\right]$$

But why does $R_z$ come first??

It doesn’t, you muppet. Think of it as functions. If you want to apply $f$ and then $g$, you would write $g(f(x))$, right?

So, if I apply rotation on X axis first and then on Y axis, I get $R=R_y(r)\times R_x(p)$. To get accelerations, multiply by gravity vector $[0,0,g{]}^T$(assuming gravity points down z-axis initially).

$$\left[\begin{array}{c}{a}_x\\ a_y\\ a_z\end{array}\right]=\left[\begin{array}{ccc}\cos r& 0& \sin r\\ 0& 1& 0\\ -\sin r& 0& \cos r\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos p& -\sin p\\ 0& \sin p& \cos p\end{array}\right]\left[\begin{array}{c}0\\ 0\\ g\end{array}\right]=\left[\begin{array}{c}g\cos r\sin p\\ -g\sin p\\ g\cos r\cos p\end{array}\right]$$

Small exercise: Angular Velocities

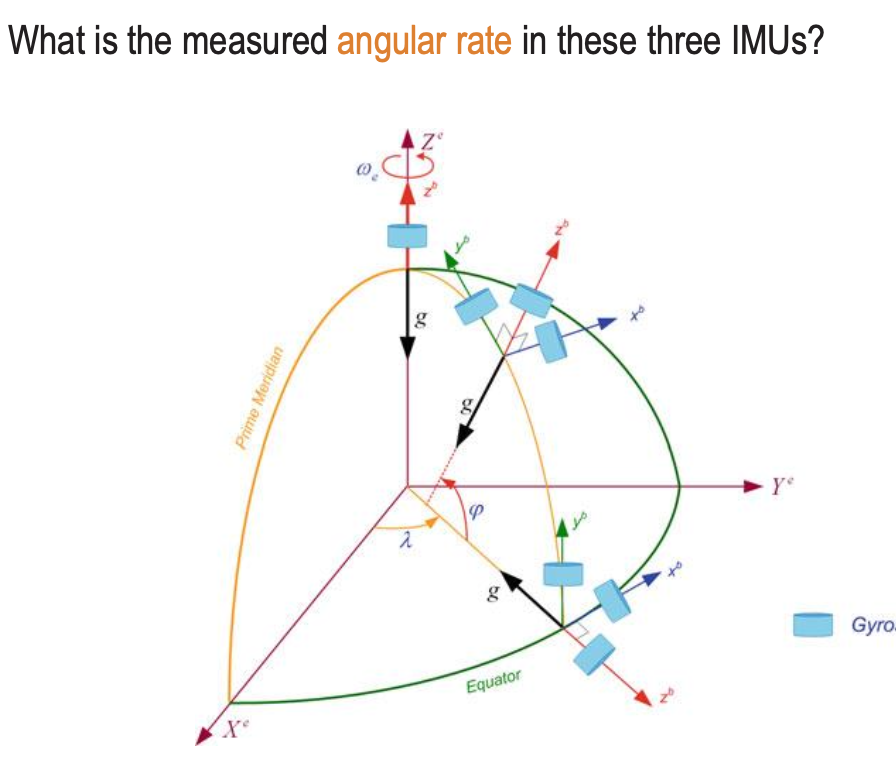
• Considering that Z points is the pure vertical.
• The earth only rotates East-West (y axis) and vertically (z axis)
• ${\omega }_x$ will be 0 for all cases.
• ${\omega }_y$ takes values for Equator (Earth’s rotation along the y-axis, tangent to surface) and for Arbitrary position
• ${\omega }_z$ takes values for North Pole and arbitrary position

	Equator	Arbitrary position*	North pole
ω_x	0	0	0
ω_y	ω_e	cos(ω_e)	0
ω_z	0	sin(ω_e)	ω_e

Note: if the direction of the true north is unknown, but the z axis is still pointing upwards, we may write

${\omega }_{xy}=\sqrt{{\omega }_x^2+{\omega }_y^2}=\cos {\omega }_e$

${\omega }_z=\sin {\omega }_e$

Since it is not known how the cos component is divided between x and y axes, this holds because ${\sin }^2\alpha +{\cos }^2\alpha =1$

Safe to say I don’t really understand what this all is. I will just stick to the first question I asked above.