Generalized Normal Distribution

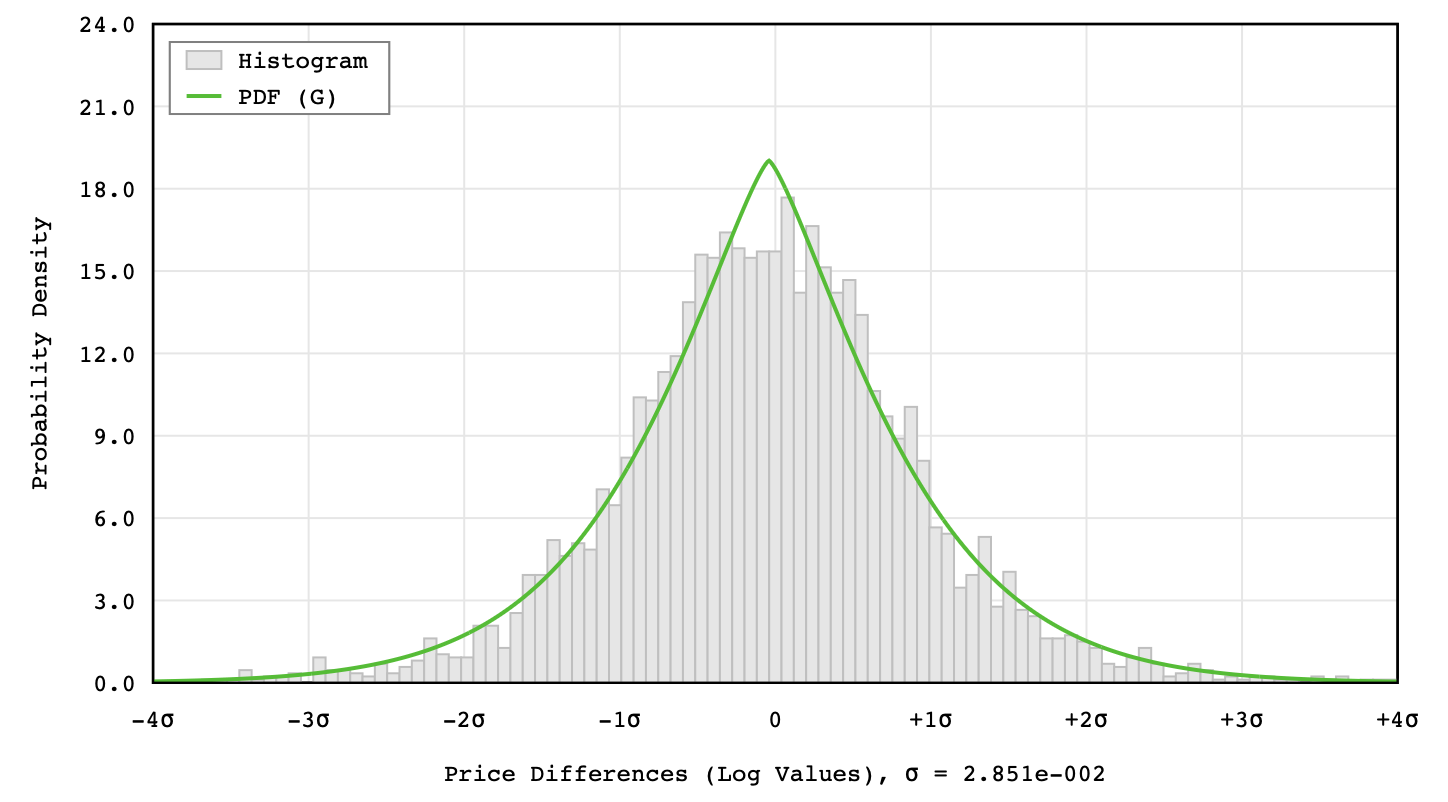
Source: https://jkillingsworth.com/2022/07/07/generalized-normal-distributions/

First encountered it in the optimal estimation subject. I had to use it to model some small uncertainty of a “softly bounded” interval of likely depths when measuring them with some prior knowledge $p(x)$.

$$p(x)=\frac{\beta }{2\alpha \Gamma \left(\frac{1}{\beta }\right)}\exp \left(-{\left(\frac{|x-\mu |}{\alpha }\right)}^{\beta }\right)$$

Mathematically, the Standard Normal is just a specific case of the Generalized version with $\beta =2$ and $\alpha =2\sqrt{\sigma }$.

• $\mu$ is the location parameter. It can be both positive and negative
• $\alpha$ is the scale parameter. Always positive
• $\beta$ is the shape parameter. Always positive

The Gamma $\Gamma$ function acts as a normalization constant to ensure the total area under the probability density function PDF $p(x)$ equals to 1.

$$\Gamma (n)={\int }_0^{\infty }{x}^{n-1}{e}^{-x}dx$$

In my case, the value $\Gamma (1/\beta )$ adjusts the scale of the distribution based on the shape parameter β so that the probabilities remain valid regardless of how “flat” or “pointed” the curve becomes.

The gen­er­al­ized nor­mal dis­tri­b­u­tion can al­so take the form of a uni­form dis­tri­b­u­tion as the shape pa­ra­me­ter ap­proach­es in­fin­i­ty.

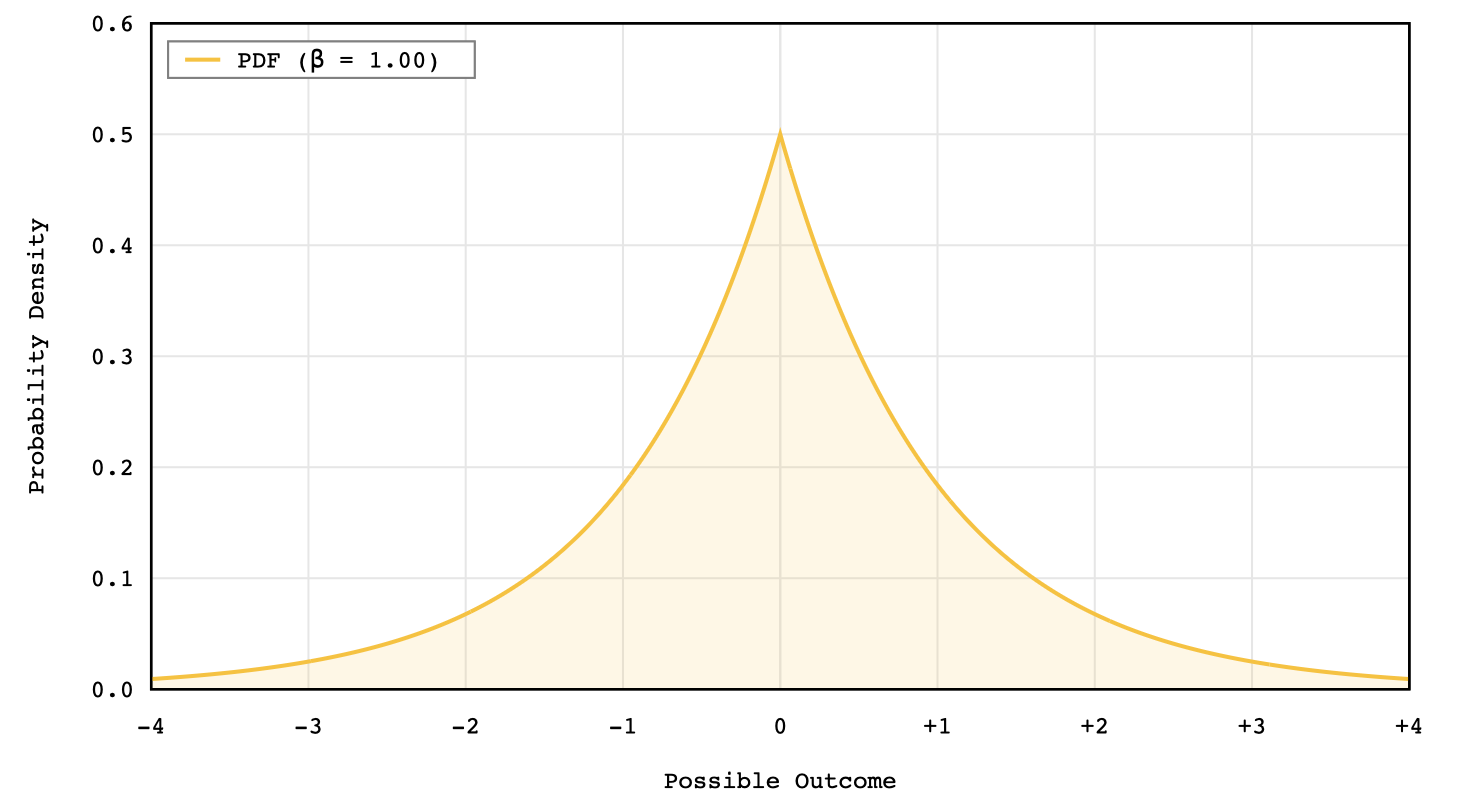
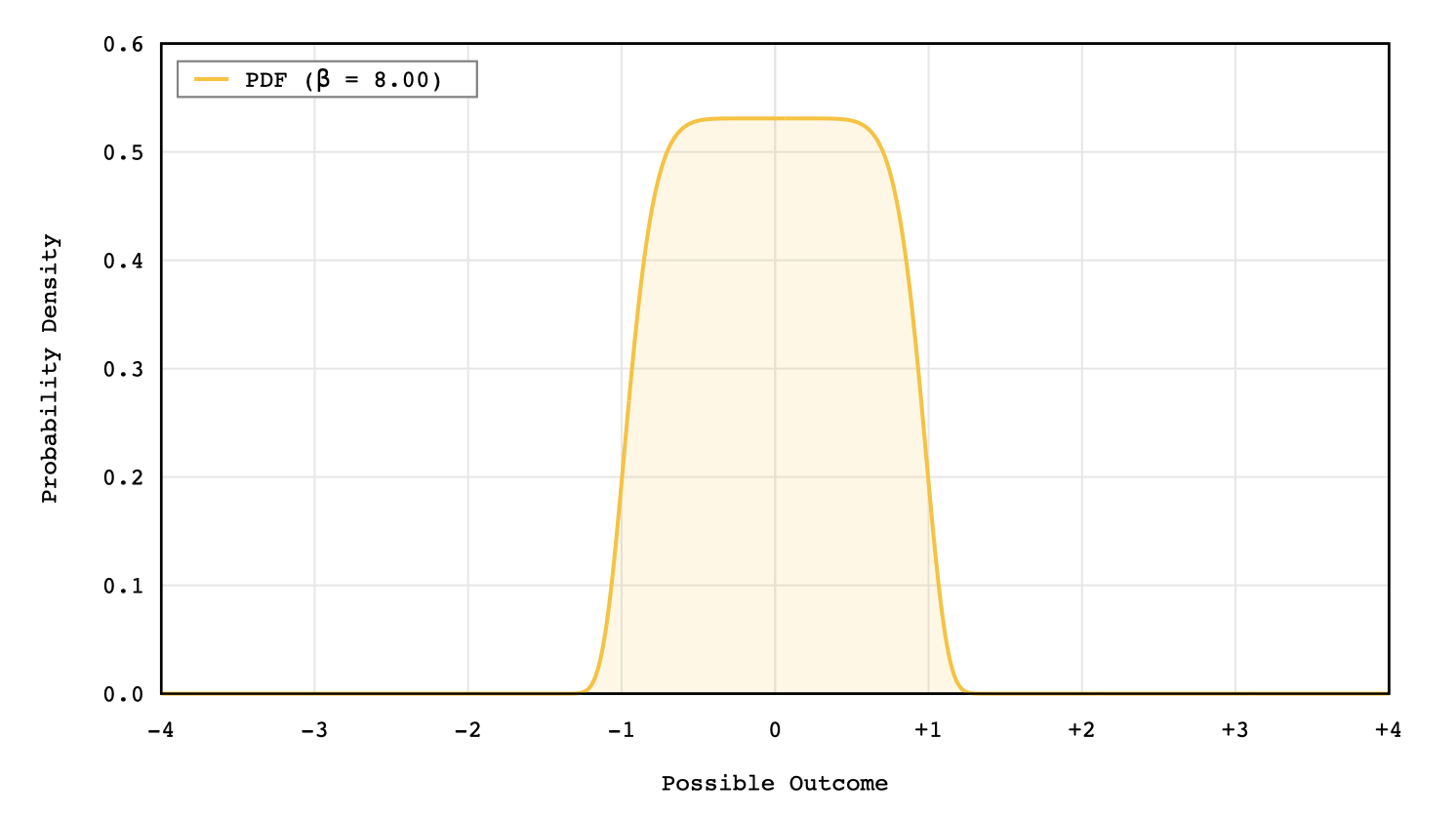
Numerical Parameter Estimation

If you have a set of ob­served da­ta that is dis­trib­uted ac­cord­ing to a known prob­a­bil­i­ty dis­tri­b­u­tion, you can use the max­i­mum like­li­hood method to es­ti­mate the pa­ra­me­ters of the dis­tri­b­u­tion.

If the dis­tri­b­u­tion is a nor­mal dis­tri­b­u­tion, the pa­ra­me­ter val­ues can be solved for an­a­lyt­i­cal­ly by tak­ing the par­tial de­riv­a­tive of the like­li­hood func­tion with re­spect to each one of the pa­ra­me­ter­s.

To fit the gen­er­al­ized nor­mal dis­tri­b­u­tion to an ob­served set of data, we need to find the pa­ra­me­ter val­ues that max­i­mize this func­tion. In­stead of com­ing up with an an­a­lyt­i­cal so­lu­tion, we can use a nu­mer­i­cal op­ti­miza­tion method. Tak­ing this ap­proach, we need to come up with a cost func­tion that our op­ti­miza­tion method can eval­u­ate it­er­a­tive­ly.

By doing this, we will be able to fit the data by finding the parameters $\beta$ and $\sigma$.