Human Robot Interaction

The structure will be:

• Robot and Human modelling
• Intention detection and expression
• Verbal communication
• Decision making
• Learning human behavior
• Task sharing and use cases
• Safety and ergonomics
• Ethics

Lecture 1: Introduction

HRI = even more interdisciplinary than Robotics because we take the social world in consideration and the interactions the robot has with humans.

HRI

• Robotics,
• Philosophy,
• Humans,
• Design,
• AI,
• HCI (Human Computer Interaction) i.e. Sociology & Anthropology

Robotics $\leftarrow$ Robots navigate and manipulate the physical world

HRI $\leftarrow$ Robots interact with people in the social world

There’s levels to this shit

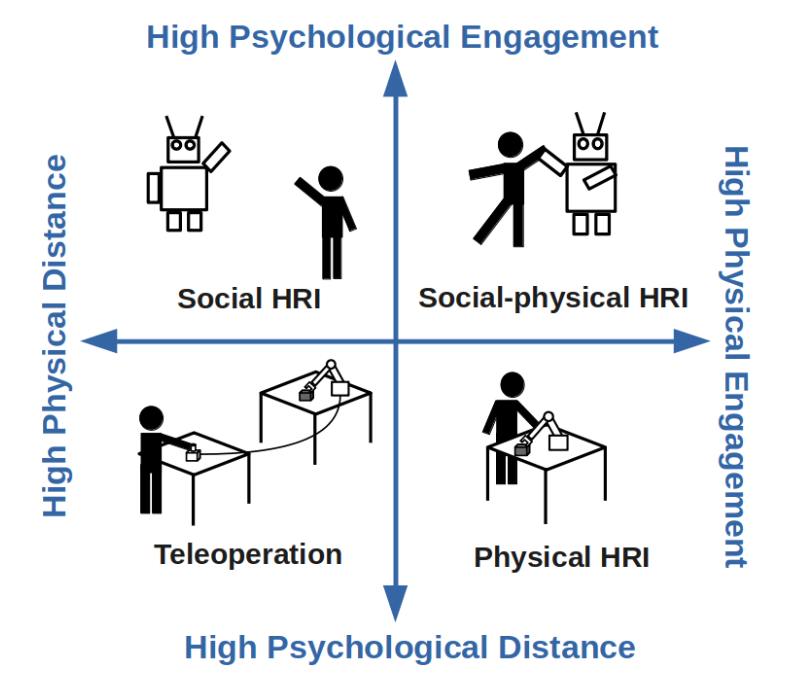
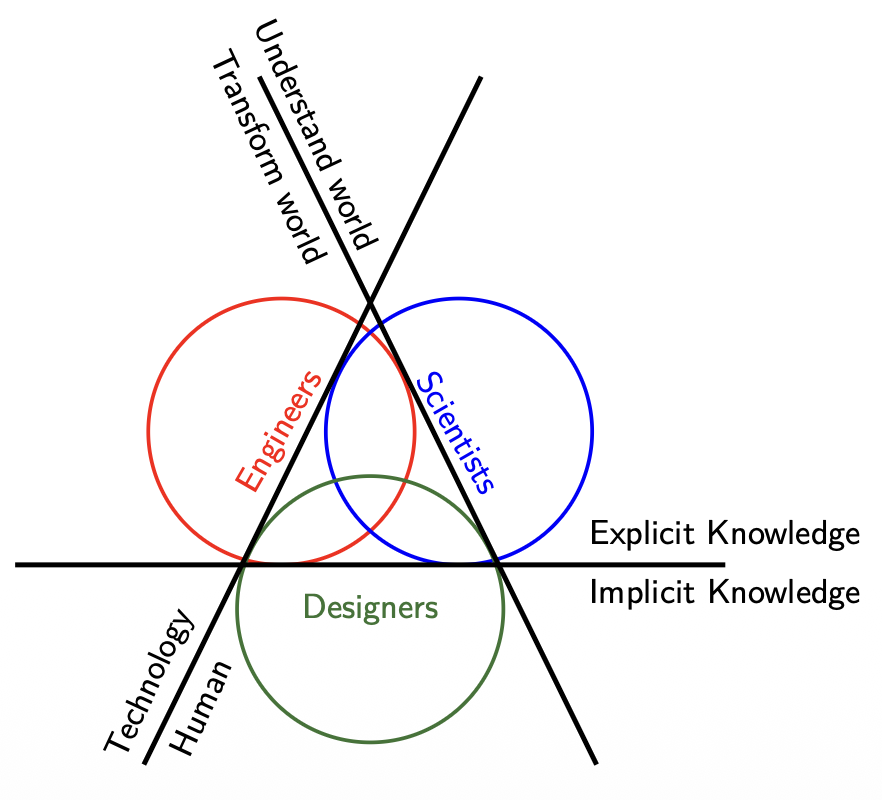
• Scientists combine the goal of Understanding the World with Explicit Knowledge to develop theories on how humans perceive robots and use the Human axis to conduct controlled behavioral studies.
• Engineers focus on Transforming the World through Technology and Explicit Knowledge, prioritizing the development of robust hardware and reliable software architectures that allow the robot to function.
• Designers bridge the gap by utilizing Implicit Knowledge and the Human axis to ensure the interaction is intuitive, focusing on the "how it feels" aspect of the robot's presence in a social environment.

Lecture 2: Robot Modelling

Robot Modelling

• Robot morphology and types
• Sensors and outputs
• Kinematics
• Challenges

Therefore, we could define a robot as an autonomous machine capable of sensing its environment, carrying out computations to make decisions, and performing actions in the real world.

Hardware: Robot Morphology

The Uncanny Valley is a critical concept in HRI that dictates how important robot morphology is.

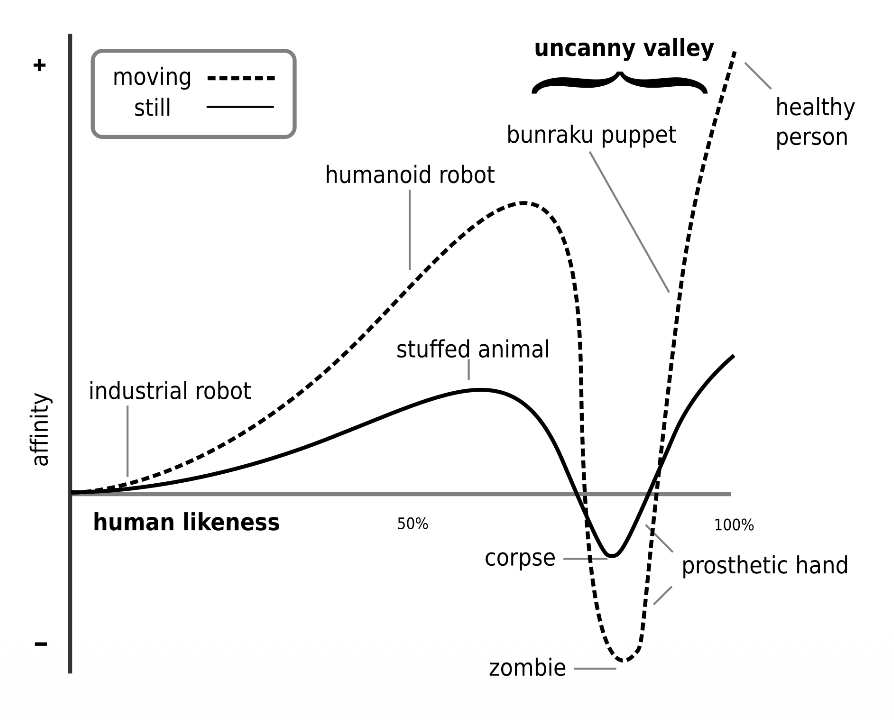
• Affinity and Likeness: As a robot becomes more human-like, our affinity for it increases.
• The Dip: When a robot is “almost” human but not quite perfect, there is a sharp drop in affinity where it becomes creepy or repulsive (labeled as “corpse” or “zombie” levels).
• The Movement Multiplier: Movement (the dashed line) amplifies these feelings. A likable robot becomes more endearing when it moves, but a creepy robot becomes significantly more disturbing.

Software: Sensors and outputs

Here we have 3 possible architectures:

• Reactive (simply sense using the sensors and then act using actuators). Open loop.
• Sense-Plant-Act (Introduce the Planning phase to the prior concept). It’s also closed-loop.
• Behavior-Based (Here we already have decision-making abilities such as avoiding objects or exploring the world).

Robot Modelling: Forward Kinematics

We describe the pose of the end-effector using a 4x4 transformation matrix (affine transformation — it makes transformations from one state to another simpler by combining the Rotation and Translation vectors into one matrix)

$$T=\left[\begin{array}{cc}3\times 3& 3\times 1\\ 1\times 3& 1\times 1\end{array}\right]=\left[\begin{array}{cccc}& & & posi\\ & orientation& & -\\ & & & tion\\ 0& 0& 0& 1\end{array}\right]$$

Forward Kinematics is the process of calculating the final position and orientation of the end effector (the robot’s “hand”) based on the angles of its joints ($q$) and the lengths of its links ($l$).

• Chaining Transformations: We calculate individual transformation matrices for each joint $(R_0^1,R_1^2,R_2^3,R_3^4$) and multiply them together to get the total transformation $(R_0^4)$.
• The final matrix is a function of joint positions $(q_1,q_2,q_3)$ and link lengths $(l_1,l_2,l_3)$.

Example

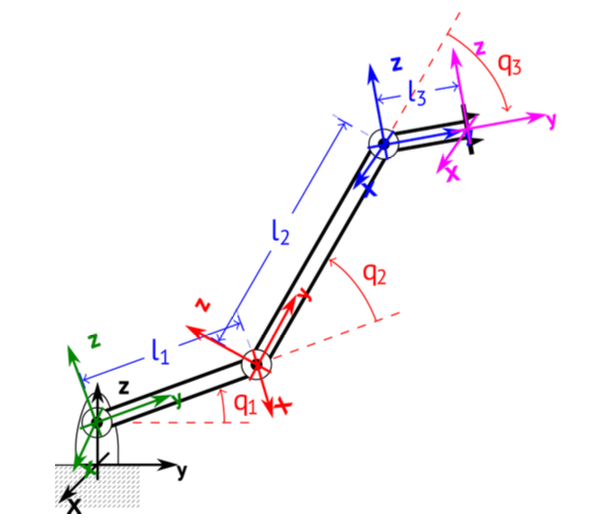
Simply understand what each value represents in the following steps and where it should be inserted if we want a Rotation around an axis or a translation along another.

Step 1: Base Frame to Joint 1

This represents a translation along the Z-axis and a rotation around the X-axis.

$$R_0^1=Trans(Z,1)R(X,q_1)=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 1\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& c_1& -s_1& 0\\ 0& s_1& c_1& 0\\ 0& 0& 0& 1\end{array}\right]$$

Step 2: Joint 1 to Joint 2

This involves a translation along the Y-axis by the length of the first link (l1​) and a rotation around the X-axis.

$$R_1^2=Trans(Y,l_1)R(X,q_2)=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& l_1\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& c_2& -s_2& 0\\ 0& s_2& c_2& 0\\ 0& 0& 0& 1\end{array}\right]$$

Step 3: Joint 2 to Joint 3

This follows the same pattern, translating by link length $l_2$​ and rotating by joint angle $q_3$​.

$$R_2^3=Trans(Y,l_2)R(X,q_3)=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& l_2\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& c_3& -s_3& 0\\ 0& s_3& c_3& 0\\ 0& 0& 0& 1\end{array}\right]$$

Step 4: Final Tool Tip Translation

This final matrix accounts for the length of the end effector link ($l_3$​).

$$R_3^4=Trans(Y,l_3)=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& l_3\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

Final Result: Forward Kinematics Matrix ($R_0^4$​)

This is the combined matrix representing the total position and orientation of the end effector relative to the base.

$$R_0^4=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& c_{1,2,3}& -s_{1,2,3}& l_3{c}_{1,2,3}+l_2{c}_{1,2}+l_1{c}_1\\ 0& s_{1,2,3}& c_{1,2,3}& l_3{s}_{1,2,3}+l_2{s}_{1,2}+l_1{s}_1+1\\ 0& 0& 0& 1\end{array}\right]$$

Therefore, we can deduce the definition:

Forward Kinematics

The FKM is a transformation matrix, a function of the joint positions and link lengths. If we know these variables, we can calculate the position and orientation of the end effector (or any other point).

Denavit-Hartenberg (DH) convention

The Denavit-Hartenberg convention define the relationship between consecutive joint frames, specifically from joint $i$ to joint $i+1$. It reduces the transformation between links to four specific parameters.

• $d_i$​ (Joint offset): The length along the Z-axis from joint i to joint i+1.
• ${\theta }_i$​ (Joint angle): The rotation around the Z-axis between joint i and joint i+1.
• $r_i$​ (Link length): The distance along the X-axis from joint i to joint i+1.
• ${\alpha }_i$​ (Link twist): The angle around the X-axis from joint i to joint i+1.

$$T_i^{i+1}=Rx({\alpha }_i)\cdot Tx(r_i)\cdot Rz({\theta }_i)\cdot Tz(d_i)$$

Robot Velocity: The Jacobian

The Jacobian is specifically defined as a $6\times n$ matrix, where $n$ is the number of joint velocities. It relates joint velocities ($\dot{q}$​) to the 6D end-effector velocity vector ($\zeta$) consisting of three linear velocities ($u$) and three angular velocities ($\omega$).

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{z}\\ {\omega }_x\\ {\omega }_y\\ {\omega }_z\end{array}\right]=\xi =J\dot{q}=J\left[\begin{array}{c}{\dot{q}}_1\\ {\dot{q}}_2\\ ⋮\\ {\dot{q}}_n\end{array}\right]$$

Inverse Kinematics

The primary distinction between the two models is the direction of the calculation:

Difference between Forward and Inverse Kinematics

• Forward Kinematics: specific coordinate values are given to each joint $\to$ where the end-effector will be located
• Inverse Kinematics: desired end-effector position $\to$ what the joint coordinate values should be

$$g(P_x,P_y,P_z,\varphi ,\theta ,\psi )\mapsto q=[q_1,q_2,\dots ,q_n]$$

As a rule of thumb, the end-effector is the terminal component that facilitates the robot’s interaction with its environment to accomplish its specific mission.

Example of Forward and Inverse Kinematics Modelling for a mobile robot (differential drive)

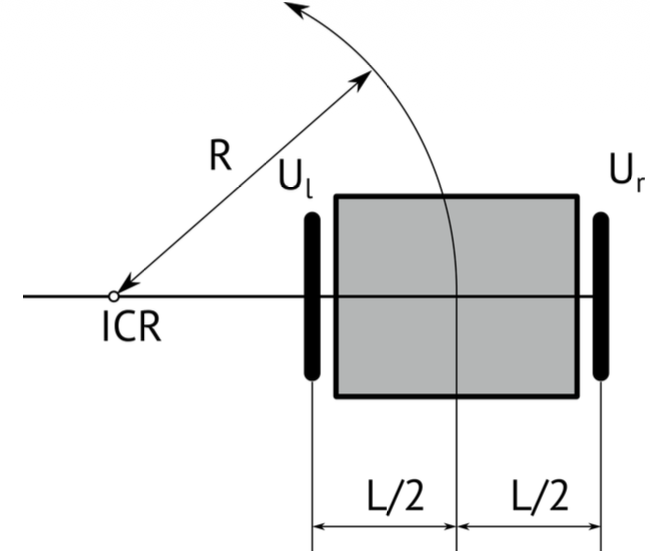
The robot’s state in the environment is defined by its Pose ($P$), and its movement is dictated by the Control Input ($U$).

• Pose ($P$): The robot’s position $(x,y)$ and its orientation angle $(\theta )$ in the global frame.
• Control Input ($U$): Consists of the robot’s linear velocity ($U$) and its angular velocity ($\Omega$).

In differential drive, to follow a trajectory, the robot rotates around an Instantaneous Center of Rotation (ICR) which is the point around which the robot appears to be rotating at a specific moment.

Rotation Radius (R): The distance from the ICR to the center of the robot. It is determined by the wheel velocities $(U_r,U_l)$ and the distance between wheels $(L)$.

Forward Kinematics:

If we define $r=U_r+U_l$, the final step combines these relations into a single matrix that maps the rotational velocities of the wheels $({\omega }_r,{\omega }_l)$ to the robot’s overall velocities $(U,\Omega )$.

$$\left[\begin{array}{c}U\\ \Omega \end{array}\right]=\left[\begin{array}{cc}\frac{r}{2}& \frac{r}{2}\\ \frac{r}{L}& \frac{-r}{L}\end{array}\right]\left[\begin{array}{c}{\omega }_r\\ {\omega }_l\end{array}\right]$$

Inverse Kinematics:

Inverse kinematics for a differential drive robot involves calculating the individual wheel velocities (${\omega }_r,{\omega }_l$​) required to achieve a desired global robot motion $(U,\Omega )$ or a specific rotation radius $(R)$.

$${\omega }_r=\Omega \frac{R+\frac{L}{2}}{r}=U\frac{1+\frac{L}{2R}}{r}$$ $${\omega }_l=\Omega \frac{R-\frac{L}{2}}{r}=U\frac{1-\frac{L}{2R}}{r}$$

It’s basically writing the output in terms of the input.

And if we define the kinematics model in the world frame in terms of a homogenous transformation, we get

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{cc}\cos \theta & 0\\ \sin \theta & 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}U\\ \Omega \end{array}\right]=\left[\begin{array}{cc}\cos \theta & 0\\ \sin \theta & 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}\frac{r}{2}& \frac{r}{2}\\ \frac{r}{L}& -\frac{r}{L}\end{array}\right]\left[\begin{array}{c}{\omega }_r\\ {\omega }_l\end{array}\right]=\left[\begin{array}{cc}\frac{r\cos \theta }{2}& \frac{r\cos \theta }{2}\\ \frac{r\sin \theta }{2}& \frac{r\sin \theta }{2}\\ \frac{r}{L}& -\frac{r}{L}\end{array}\right]\left[\begin{array}{c}{\omega }_r\\ {\omega }_l\end{array}\right]$$

How do we estimate the pose when we have noise? Slap a Kalman Filter

$$X_k=A{X}_{k-1}+B{U}_{k-1}+w_k$$ $$Y_k=H{X}_k+v_k$$

where $w_k$ is the process noise and $v_k$ is the measurement noise

The noise signals $w_k$, $v_k$ are considered to be normally distributed with zero means and covariance matrices $Q$ and $R$ respectively. We talk about covariance when we have multiple states and we have to estimate noise for each of them.

Basically, it’s a way to introduce uncertainty in our modelling.

In the ROS ecosystem, localization is organized through a standardized hierarchy of coordinate frames to ensure different sensors and algorithms can communicate effectively. This structure follows a specific chain: earth $\to$ map $\to$ odom $\to$ base_link.

• earth: Can be used for connecting multiple robots on different maps
• map: Calculated based on discontinuous sensors (e.g. GPS)
• odom: Calculated based on continuous sensors, (e.g. IMUs)
• base_link: Attached on the robot, as forward, left, up

There are also two ROS standard systems:

• REP 103: Defines standard units of measure and coordinate conventions.
• REP 105: Specifically defines the coordinate frames for mobile platforms mentioned above.

Lagrangian of a robot

The Lagrangian of a robot provides a condensed way to describe its dynamic behavior, relating the forces or torques acting on the joints to the resulting motion.

The general dynamic equation:

$$D(q)\ddot{q}+C(q,\dot{q})\dot{q}+g(q)=\tau$$

• The matrix $D$, contains information about the inertia of the system, therefore contains all the masses and moments of inertia.
• The matrix $C$ has elements related to the centrifugal and Coriolis terms.
• $g(q)$ (Gravity Vector): This term represents the dependence of the robot’s potential energy on its position, accounting for gravity.
• $\tau$ (Torque): The vector of generalized forces or torques applied to the joints

This equation above is the inverse dynamics where we want to know what torque $\tau$ should be applied to achieve a specific acceleration $\ddot{q}$. You use this to determine how much power your motors must output to move the robot in a specific way.

The forward dynamics tells us what acceleration $\ddot{q}$ we get if we apply a specific torque $\tau$. You use this primarily for simulation to see how the robot will actually react to motor inputs.

$$\ddot{q}=D(q{)}^{-1}\left(\tau -C(q,\dot{q})\dot{q}-g(q)\right)$$